Popularity Signals in Trial-Offer Markets with Social Influence and Position Bias
Abstract
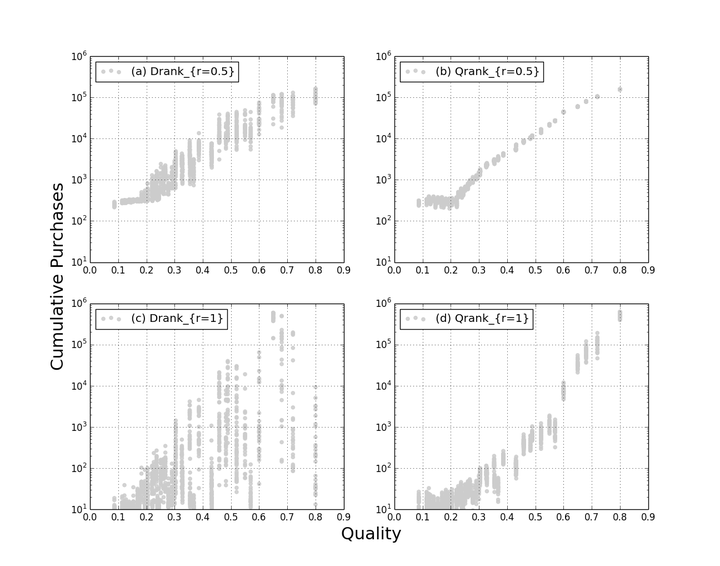
This paper considers trial-offer markets where consumer preferences are modelled by a multinomial logit with social influence and position bias. The social signal for a product is given by its current market share raised to power r (or, equivalently, the number of purchases raised to the power of r). The paper shows that, when r is strictly between 0 and 1, and a static position assignment (e.g., a quality ranking) is used, the market converges to a unique equilibrium where the market shares depend only on product quality, not their initial appeals or the early dynamics. When r is greater than 1, the market becomes unpredictable. In many cases, the market goes to a monopoly for some product: which product becomes a monopoly depends on the initial conditions of the market. These theoretical results are complemented by an agent-based simulation which indicates that convergence is fast when r is between 0 and 1, and that the quality ranking dominates the well-known popularity ranking in terms of market efficiency. These results shed a new light on the role of social influence which is often blamed for unpredictability, inequalities, and inefficiencies in markets. In contrast, this paper shows that, with a proper social signal and position assignment for the products, the market becomes predictable, and inequalities and inefficiencies can be controlled appropriately.